受 CFDwired 之邀,在 CFDwired Forum 开办 Code of the Week (每周一行 (háng)),还请各位大佬,CFD/OpenFOAM 用家多多包涵,班门弄斧了。
Code of the Week #1: div(phi,U)
我们现在讨论一下这一行程序
fvm::div(phi, U);
这个经常出现在动量方程,表示左边第二项
为了求解这个方程,需要经过一些推导,并对 p 和 U 进行解耦。但是,今天我们暂时不要讨论如何解耦。只讨论一下如何把 \nabla\cdot(UU) 变成可进行计算的一小段程序。
实际上,动量方程是一个非线性的方程,但是直接求解这样一个非线性的方程,是很困难的。
因此,我们考虑将其中一个 U 当成已知的 U^* ,则
而使用有限体积法时,需要对方程进行积分,这一项也不例外,这里考虑空间积分,
d S 是离散单元的面,是有方向的。 \vec{F} 就是通量,用已知的 U^* 计算。
获得这一公式后,需要完成某一网格上的格式,此格式就是对流格式。
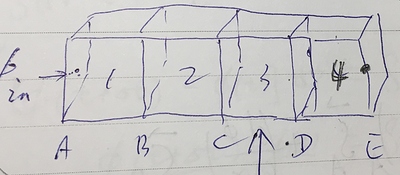
比如,考虑这样一个一维情况,有四个均分网格,编号 1 – 4,其左右的面从左到右依次为 A – E,在第 3 个网格上:
div(phi,U) 就是实现上面这个公式。
但是,要真正地实现可计算,还有几步要完成。首先,待求的值一般是指体心的值,而 \varphi_C 是指面 C 上的值,而我们并不知道,因此,就需要插值,如果考虑以该面的相邻两个网格的线性平均值为该面上的值,这一插值方法称为中心差分,则
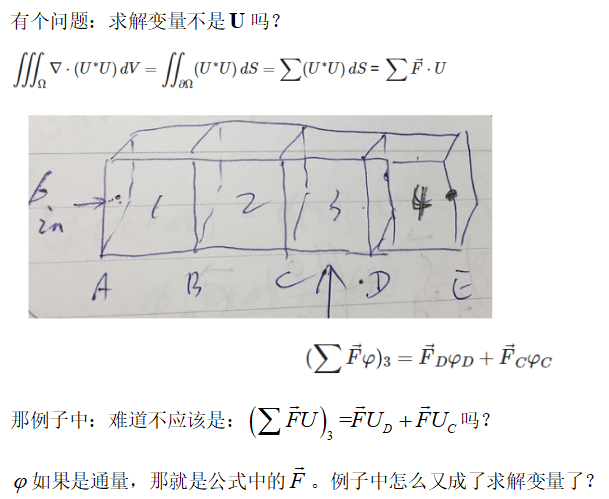
当 U^* 在整个空间都是相同的时候,针对控制体 3 时, -\vec{F}_C=\vec{F}_D ,通量方向规定为:向外为正,向内为负,因此,有
不知道大家留意到没,我们需要求的变量 \varphi_3 不见了。
对于边界 A,设已知 \varphi_A ,对于网格 1,有 -\varphi_A + \dfrac{\varphi_1+\varphi_2}{2} 。
对于边界 E,设 \varphi_E=\varphi_4 ,对于网格 4,有 -\dfrac{\varphi_3+\varphi_4}{2}+\varphi_E=-\dfrac{\varphi_3+\varphi_4}{2}+\varphi_4
这四个网格,可组成一个矩阵乘法,
这一项再和动量方程的其他项相加,就可以完成该方程的离散化,可用矩阵计算的方法获得 \varphi_i 的数值解。
对于获得面上的值的插值方法,在 OpenFOAM 中,其指定的方式是在 ./system/fvSchemes 里面的,如
divSchemes
{
div(phi,U) Gauss linear;
}
其中, Gauss 指的就是 \sum 的方法,linear 就是插值的方法,但是,值得注意的地方就是对流项最少使用中心差分,主要原因是易形成矩阵主元除边界上的外,其他都为 0,这会造成矩阵求解困难。
在 OpenFOAM 的程序中,div 前面还有 fvm::,fvm 表明该项表达式返回的值是矩阵系数。
如写成另外一种形式 fvc::div(phi,U) 则表明返回的是 \nabla(UU) 的值。
:: 是 C++ 的作用域符,是运算符中等级最高的,它分为三种:
- global scope (全局作用域符),用法 (::name)
- class scope (类作用域符),用法 (class::name)
- namespace scope (命名空间作用域符),用法 (namespace::name)
他们的作用都是为了明确的调用你想要的变量。